I am a 4th-year undergraduate in Computational Mathematics at Peking University. Seeking USA PhD 26Fall. My research lies at the intersection of high-dimensional PDEs, scientific ML, diffusion models, and quantum/non-equilibrium Markov dynamics. I build theory-backed algorithms and scale them to high-dimensional experiments.
Here is my CV.
🔥 News
- Feb 2026 — Physics-Informed Inference-Time Scaling for Solving High-dimensional PDE via Simulation-Calibrated Scientific Machine Learning (SCaSML) is accepted by ICLR2026.
📝 Publications
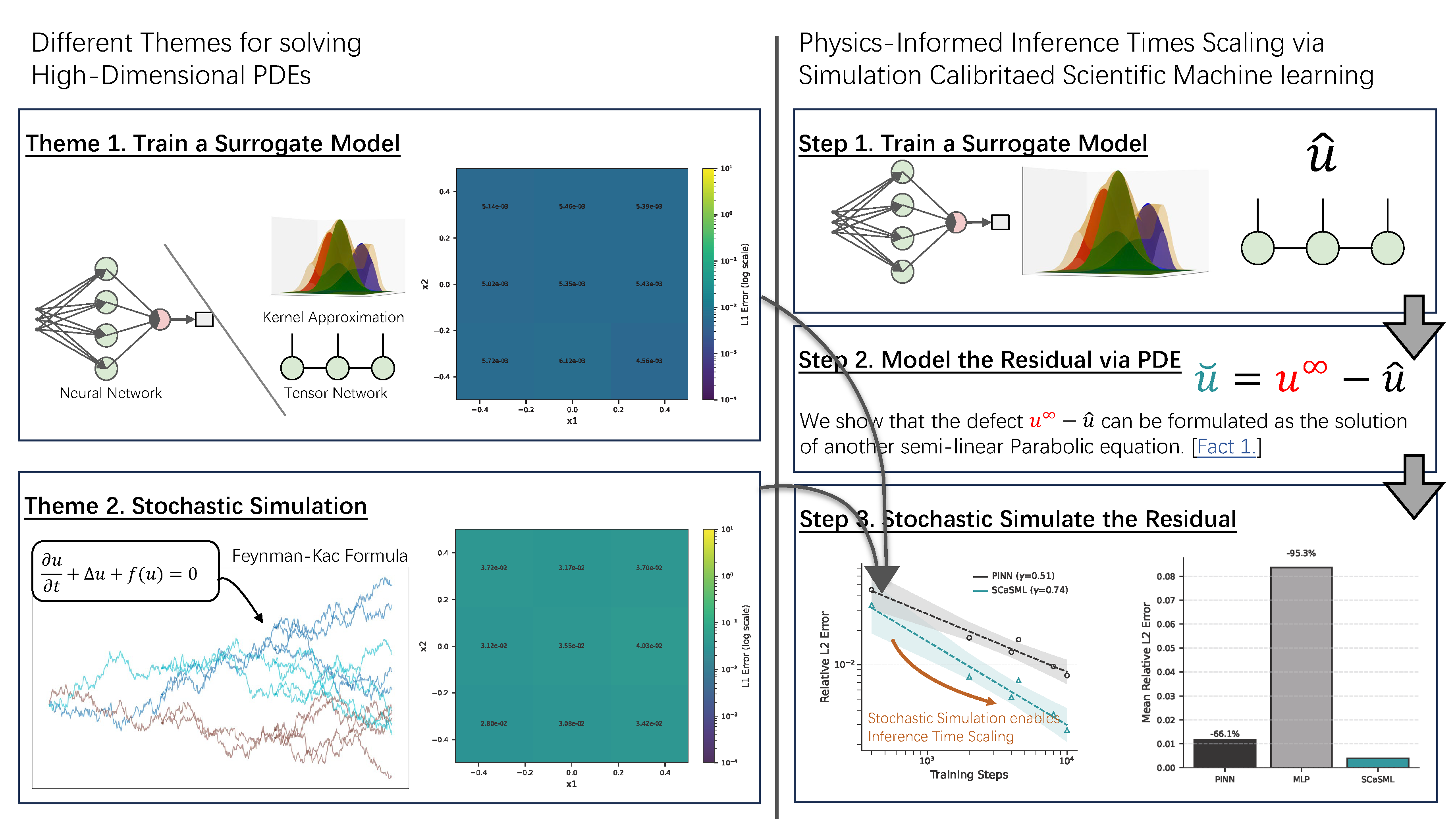
Authors: Zexi Fan, Yan Sun, Shihao Yang, Yiping Lu
- First inference-time PDE solver that uses a surrogate (PINN) calibrated by simulation with provable convergence improvements.
- Demonstrated numerical efficacy on multiple semi-linear, gradient-dependent PDE systems at high dimensions (100d+); accompanying code and experiments available.
🎖 Honors and Awards
(to be filled / updated)
📖 Education
- Sep 2022 - Present, Peking University (PKU), B.S. in Computational Mathematics
- Major GPA: 3.6 / 4.0
- Selected Courses: Abstract Algebra (93), Machine Learning (93), Advanced Algebra II (90)
- Advanced mathematical training: Stochastic Analysis & Control, Scientific Machine Learning, PDEs
- GRE: 164(Q) / 169(V) / 4.0(A) (Aug 2023)
💬 Invited Talks
(to be updated when scheduled)
💻 Internships
(to be updated)
🔬 Research Experience
Accelerating NESS sampling on Quantum Markov Chains via Second-Order Lifting — Jul 2025 – Present
- Supervisors: Prof. Jianfeng Lu (Duke), Prof. Bowen Li (CityU)
- Overview: Designed a second-order lifting framework to accelerate sampling of Non-Equilibrium Steady States (NESS) for Lindbladian dynamics. (In preparation version: link)
- Key contributions:
- Introduced a second-order lifting for Lindbladian dynamics; used hypocoercivity and flow-Poincaré techniques to derive provable mixing acceleration to non-equilibrium steady states (NESS).
- Derived singular-value-gap bounds and validated speedups on representative quantum Markov chains via numerical experiments.
- Impact: Provides a theoretically grounded and practically implementable path to faster NESS sampling.
Continuous-State Contextual Bandit with Pessimism Regularization — Aug 2024 – Nov 2025
- Supervisor: Prof. Ying Jin (Harvard)
- Overview: Extended pessimism regularization to continuous state and action spaces with function approximation. (Note: link)
- Key contributions:
- Extended pessimism regularization to continuous state/action settings; designed a practical algorithm with confidence penalties adapted to compact action spaces.
- Proved regret guarantees removing the uniform-overlap requirement; developed concentration bounds for continuous policies.
- Impact: Bridges theoretical pessimism principles and practical continuous action bandit learning, relevant to safe RL and policy estimation in continuous environments.
Simulation-Calibrated Scientific Machine Learning (SCaSML) for High-Dimensional PDEs — Jun 2024 – Apr 2025
- Supervisors: Prof. Yiping Lu, Dr. Yan Sun (Northwestern / Georgia Tech)
- Overview: Proposed SCaSML, a pipeline that uses simulation-based estimators to calibrate surrogate PINN solutions and correct bias via Multilevel Picard (MLP) style calibration and randomized MLMC. (Paper: link)
- Key contributions:
- Derived theoretical complexity and convergence improvements showing better scaling in dimension than vanilla PINNs for a class of semilinear/parabolic PDEs.
- Proved the efficiency of such calibration rigorously using techniques from Multilevel Picard Iteration.
- Demonstrated improved complexity scaling on 100d+ benchmarks; released code and benchmarks: github.com/Francis-Fan-create/SCaSML.
- Impact: Demonstrates a viable route for inference-time/scalable PDE solving using theory-informed ML surrogates — of direct interest to groups working on scientific ML and high-dimensional computation.
Flow-Calibrated RL for Transition Path Sampling — Feb 2024 – Jun 2024
- Supervisors: Prof. Yiping Lu, Dr. Dinghuai Zhang (NYU / Mila)
- Reformulated transition-path sampling as stochastic optimal control and developed continuous Soft Actor-Critic and GFlowNet variants guided by flow-based calibration. (Slides & notes: link)
Unbiased Square-Root Convergent Estimation for High-Dimensional Semilinear Parabolic Heat Equation — Sep 2023 – Feb 2024
- Supervisor: Prof. Yiping Lu (NYU)
- Developed an unbiased estimator combining Multilevel Picard iteration with randomized MLMC and established unbiasedness and variance bounds.
📚 Academic Activities
- Graduate course: Combinatorics (Score: 92), Prof. Chunwei Song — Spring 2023
- Graduate course: Machine Learning (Score: 93), Prof. Kedian Mou — Fall 2023
- Graduate course: High Dimensional Probability, Prof. Zhihua Zhang — Fall 2024
- Graduate course: Optimization Methods, Prof. Zaiwen Wen — Fall 2024
- Graduate course: Applied Stochastic Analysis, Prof. Tiejun Li — Fall 2024
- Seminars: Blowup in fluid equations; Stochastic optimal control (organizer: Dr. Xinhan Duan); LLM & Scientific Computing (Prof. Zaiwen Wen)
- Summer school: Beauty of Theoretical Computer Science (NJU) — Summer 2024
🌐 Social Activities
- Academic & Innovation Department, SMS Student Union — Spring 2023
- English Debate Club — Summer 2024
💻 Skills / Hobbies
- Programming Languages: Python, MATLAB, \LaTeX, Markdown
- ML & Numerical Tools: PyTorch, TensorFlow, JAX, NumPy, DeepXDE, WandB
- Numerical / Math Techniques: Multilevel Picard, MLMC, Krylov solvers, reduced-order modelling, hypocoercivity, concentration inequalities, optimal transport
- Hobbies: Animation, program design
- Languages: Mandarin (native), English (fluent)
